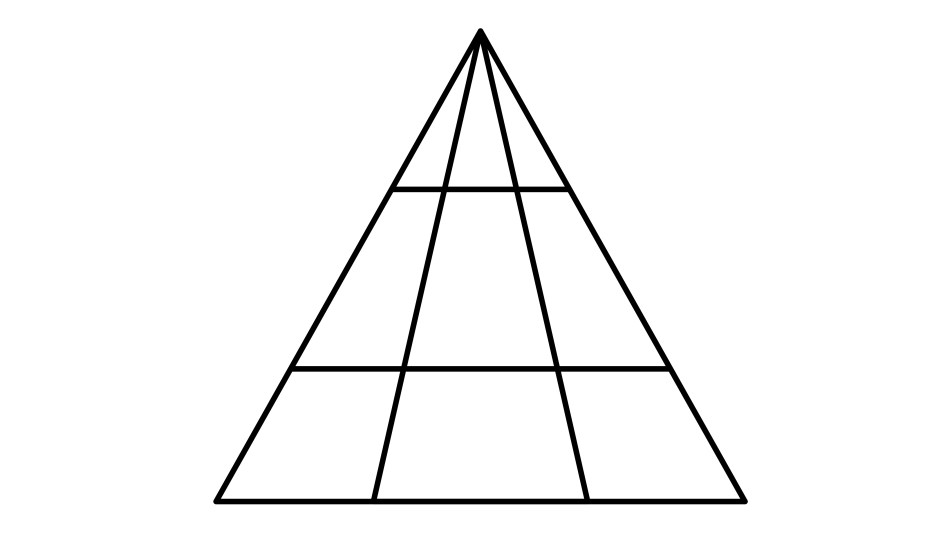
There are 24 triangles in the given figure. Now, let’s explore the interesting world of geometry and how it plays a role in our daily lives.
Geometry, a branch of mathematics, deals with the study of shapes, sizes, positions, angles, and dimensions of objects in space. It is an important subject that helps us in various fields like architecture, engineering, physics, and art. From designing buildings to creating video games, geometry is everywhere.
It teaches us how to calculate areas, volumes, and angles of different shapes, making it an essential tool for problem-solving. So, let’s embrace the power of geometry and explore its wonders.
The Fascination With Triangle Puzzles
Triangle puzzles have captivated minds for centuries, challenging our problem-solving abilities and sparking curiosity. The allure of these brainteasers lies in their intriguing patterns and the endless possibilities they offer. In this blog post, we will explore the history of brainteasers and delve into why triangles continue to capture our imagination.
The History Of Brainteasers
Brainteasers have a rich history dating back to ancient civilizations. In fact, the earliest recorded puzzle, the “Riddle of the Sphinx,” featured a triangle as its central element. Throughout the years, mathematicians, philosophers, and puzzle enthusiasts have devised various triangle puzzles to test logical reasoning and creativity.
One notable example is the “Triangle of Pythagoras” puzzle, which challenges players to arrange numbers in a triangle shape, with each cell containing the sum of the two cells above it. This puzzle, named after the famous Greek mathematician Pythagoras, highlights the enduring fascination with triangles in problem-solving.
Why Triangles Capture Our Imagination
Triangles have a unique quality that captures our imagination. Here are a few reasons why these geometric shapes continue to fascinate us:
- Visual Appeal: Triangles have a simple yet striking visual appeal that draws our attention. Their symmetrical and balanced nature makes them aesthetically pleasing.
- Challenging Patterns: Triangles offer a wide range of patterns and configurations, making them ideal for puzzle enthusiasts. From geometric patterns to number sequences, there are countless possibilities to explore.
- Symbolic Significance: Triangles hold symbolic significance in various cultures and disciplines. They represent stability, harmony, and the interconnectedness of mind, body, and spirit. This symbolism adds an extra layer of intrigue to triangle puzzles.
- Logical Reasoning: Solving triangle puzzles requires logical reasoning and critical thinking skills. As we attempt to find the patterns and connections, our problem-solving abilities are put to the test.
Whether it’s a simple triangle puzzle or a complex geometric conundrum, the fascination with triangle puzzles remains unwavering. These mind-bending challenges continue to entertain and stimulate our minds, providing endless hours of fun and mental exercise.

Credit: www.youtube.com
Basic Concepts Of Triangle Counting
When it comes to the world of puzzles, triangle counting is an intriguing and challenging concept. Understanding the basic principles of triangle counting is essential for tackling these puzzles effectively.
Types Of Triangles In Puzzles
In puzzle-solving, triangles can be categorized as upward-pointing triangles and downward-pointing triangles. The configurations of these triangles vary, presenting different challenges in the counting process.
Key Properties Of Triangles
Triangles in puzzles possess key properties such as symmetry, connectivity, and orientation. These properties impact the overall count and require careful consideration during the solving process.
Common Mistakes To Avoid
When determining the number of triangles, avoid the mistake of counting the same triangle more than once. Another common error is forgetting to include triangles formed by overlapping shapes. Be mindful of these mistakes to ensure accurate results.
When it comes to counting triangles in a complex figure, it’s easy to make mistakes. By being aware of these common errors, you can accurately determine the number of triangles in any given shape. Let’s take a look at some of the most frequent mistakes people make and how to avoid them.
Overlapping Areas
One common mistake is counting triangles that overlap or share sides. When triangles intersect, it can be tempting to count them as separate triangles. However, this can lead to an inflated count and inaccurate results. To avoid this error, carefully analyze the figure and identify triangles that share sides or overlap. Count them as one triangle instead of multiple.
Assuming Uniformity
Assuming that all triangles in a figure are identical can lead to errors. Triangles can have different sizes, orientations, and positions within a shape. By assuming uniformity, you may overlook triangles that are smaller or rotated differently. Take a closer look at each triangle and consider its unique characteristics. Don’t assume they are all the same.
Moreover, it’s important to note that not all triangles are equilateral. Equilateral triangles have three equal sides, but figures can also contain isosceles or scalene triangles, which have two or three sides of different lengths. Keep this in mind when counting triangles.
Additionally, be cautious of triangles formed by dashed or dotted lines. These lines may represent boundaries or dimensions and not actual sides of a triangle. Count only the triangles that have solid lines as their sides.
In conclusion, to accurately count triangles in a figure, avoid the common mistakes of counting overlapping areas and assuming uniformity. Pay attention to the unique characteristics of each triangle and consider the different types of triangles that may be present. By doing so, you will achieve more accurate results and avoid inflated counts. Happy triangle counting!
Step-by-step Approach To Counting Triangles
Counting triangles in complex shapes may seem daunting at first, but with a systematic approach, it becomes much simpler. By breaking down complex shapes and applying systematic counting methods, you can accurately determine the number of triangles in a given figure.
Breaking Down Complex Shapes
When faced with a complex shape, it is helpful to break it down into smaller, more manageable parts. By dividing the shape into simpler components, you can count the triangles within each part individually and then add them up to get the total count.
For example, let’s say we have a shape that consists of two overlapping triangles. To count the triangles, we can first count the triangles in each individual triangle and then add them together. This method helps us avoid missing any triangles and ensures an accurate count.
Applying Systematic Counting Methods
To count the triangles in a shape systematically, you can follow these steps:
- Start by identifying the main triangles in the shape. These are usually the larger, more prominent triangles that form the base of the figure.
- Next, look for any smaller triangles within the shape. These can be formed by lines or intersections within the figure.
- Count the triangles in each component of the shape separately. This includes triangles formed by lines, intersections, or combinations of both.
- Add up the individual counts to get the total number of triangles in the shape.
Using this systematic counting approach, you can accurately determine the number of triangles in even the most complex shapes. Remember to break down the shape into smaller parts and count the triangles within each component before adding them together.
Tips To Enhance Your Counting Skills
When it comes to counting triangles, enhancing your skills is essential for accurately solving puzzles and visual challenges. Here are some practical tips to help you enhance your counting skills:
Practice With Varied Puzzles
Engage in diverse triangle counting puzzles to sharpen your skills. Solving puzzles with different layouts and levels of complexity can help you develop a keen eye for identifying triangles in various arrangements.
Use Of Visualization Techniques
Visualize the triangles within the given shapes. Employing visualization techniques can aid in quickly recognizing patterns and formations, enabling you to count the triangles more effectively.
The Role Of Symmetry In Solving Puzzles
Symmetry plays a crucial role in solving puzzles, including the popular “How Many Triangles” conundrum. By understanding the significance of symmetry, puzzle enthusiasts can uncover efficient strategies for solving complex geometric problems. Let’s explore the influence of symmetry in unraveling the mysteries of puzzles like “How Many Triangles.”
Identifying Symmetrical Patterns
When tackling puzzles such as “How Many Triangles,” identifying symmetrical patterns is essential. Symmetry enables puzzle solvers to recognize recurring shapes and structures, paving the way for a systematic approach to counting triangles. By discerning symmetrical elements, individuals can streamline the process of identifying and enumerating triangles within the given puzzle.
How Symmetry Simplifies Counting
Symmetry simplifies the counting process by allowing puzzle solvers to leverage repetitive patterns. In the context of “How Many Triangles,” symmetry enables individuals to identify mirrored or rotated configurations, reducing the complexity of the puzzle. By capitalizing on symmetrical properties, the task of counting triangles becomes more manageable and less prone to errors.
Advanced Strategies For The Pros
For those seeking to conquer the challenge of counting triangles, advanced strategies are essential. Let’s delve into the expert techniques used by pros in the realm of geometric puzzles.
Geometric Theorems And Triangle Counting
Understanding geometric theorems is a cornerstone for mastering triangle counting.
- Pythagorean Theorem: a^2 + b^2 = c^2
- Angle Sum Property: Sum of angles in a triangle is 180 degrees
Algorithmic Approaches
Algorithmic approaches streamline triangle counting with efficiency.
- Brute Force Method: Counting triangles manually
- Graph Theory Algorithms: Utilizing graph structures for complex triangle calculations
Credit: www.womansworld.com
Interactive Triangle Puzzles And Resources
Discover a world of interactive triangle puzzles and resources that will challenge your mind and expand your geometric knowledge.
Online Puzzle Platforms
Explore various online platforms offering engaging triangle puzzles for all skill levels.
Books And Guides For Enthusiasts
Delve into comprehensive books and guides that provide in-depth insights into triangle puzzles.
The Psychological Benefits Of Puzzle Solving
Engaging in puzzle solving, such as figuring out “How Many Triangles,” offers various psychological benefits. It enhances problem-solving skills, boosts cognitive abilities, and promotes a sense of accomplishment, which can positively impact overall mental well-being.
Cognitive Advantages
Emotional And Stress-relief Benefits
The Psychological Benefits of Puzzle Solving can have a positive impact on mental well-being. Engaging in puzzles can enhance cognitive abilities. Solving puzzles can improve memory and increase problem-solving skills. It also boosts creativity and enhances critical thinking. Puzzle solving can provide a sense of accomplishment. It stimulates the brain and keeps it active. Solving puzzles can be a fun way to relax. It can reduce stress and anxiety levels. Puzzle solving promotes a sense of satisfaction and boosts mood.
Challenging Yourself: From Puzzles To Real-world Applications
Ready to dive into the intriguing world of triangles? Let’s explore how understanding triangles goes beyond puzzles and finds relevance in real-world scenarios.
Triangles In Architecture And Art
Architects and artists use triangles to create stability and balance in structures and compositions.
Educational Benefits In Mathematics
Learning about triangles enhances mathematical skills and problem-solving abilities.
Frequently Asked Questions
How Can I Calculate The Number Of Triangles In A Shape?
To calculate the number of triangles in a shape, you need to count the number of triangles formed by the intersection of the lines in the shape. Start with the smallest triangles and work your way up to the larger ones.
You can use formulas like n(n-1)(n-2)/6 to calculate the number of triangles in a shape with n vertices.
What Is The Maximum Number Of Triangles In A Shape?
The maximum number of triangles in a shape depends on the number of vertices in the shape. For a shape with n vertices, the maximum number of triangles is n(n-1)(n-2)/6. For example, a shape with 4 vertices can have a maximum of 4 triangles, while a shape with 6 vertices can have a maximum of 20 triangles.
How Many Triangles Are In A Square?
A square has a total of 2 triangles – one triangle formed by the diagonal and one formed by the square itself. So, the total number of triangles in a square is 2.
How Many Triangles Are In A Pentagon?
A pentagon has a total of 35 triangles. You can calculate this by counting the number of triangles formed by the intersection of the lines in the pentagon, starting with the smallest triangles and working your way up to the larger ones.
Conclusion
Understanding the concept of counting triangles can be both fun and challenging. By applying the proper techniques and formulas, you can easily determine the number of triangles in different shapes. Remember to practice regularly to sharpen your skills and master the art of counting triangles with precision.
Happy counting!


